嗯,作者在咕咕咕了整整一个月后又来写 A + B Problem 了……
一看题目,发现 |a| , |b| <= 1e9 , 而且 a 和 b 还都是整数,所以我们自然而然地想到了要用高精度来计算啦 [aru_7]
然而作者太菜了不会写高精度 QAQ,所以作者就用 bitset 来实现了一个 512 位整数以及对应的加法运算,加法运算的原理,就是计算机中加法器的原理。
具体的来讲,就是 a + b = (a xor b) + (a and b) * 2,其中乘以二的操作可以用左移来表示,也就是说这样的加法可以全部由位运算来实现,只不过外面要包一层循环。
该结论证明:
首先,我们观察以下算式:(其中 ^ 表示异或,数字皆为二进制)
0 ^ 0 = 0, 0 & 0 = 0, 0 + 0 = 00
1 ^ 0 = 1, 1 & 0 = 0, 1 + 0 = 01
0 ^ 1 = 1, 0 & 1 = 0, 0 + 1 = 01
1 ^ 1 = 0, 1 & 1 = 0, 1 + 1 = 10
不难发现,任意两个一位的二进制数 a 和 b 相加所得的结果一定是 (a & b) * 2 + (a ^ b)
因此,我们可以得到:
于是得证。
还有一个问题,就是如何将读入的十进制数转为二进制,以及将二进制转为十进制并输出……这个问题我们用满八减三法和满五加三法来解决。具体证明我也不太会,可以百度一下 [aru_25]
所以,这个问题就可以被“圆满”的解决了!下面贴上代码:
#include<bits/stdc++.h>
/*
* Code from vgakbzc
*/
typedef std::bitset<512> int512;
char buf[1007];
int512 StrToBCD(char* s){
int len=strlen(s);
int cur=0;
int512 res;
for(int i=len-1;i>=0;i--,cur+=4){ // String to bcd code
int x=s[i]-'0';
res[cur+0]=bool(x&1);
res[cur+1]=bool(x&2);
res[cur+2]=bool(x&4);
res[cur+3]=bool(x&8);
}
return res;
}
int512 BCDToBIN(int512 bcd){ // bcd code to binary
std::bitset<1024> tmp;
tmp.reset();
for(int i=512;i<1024;i++){
tmp[i]=bcd[i-512];
}
for(int i=0;i<512;i++){
tmp>>=1;
for(int j=512;j<1024;j+=4){
int p=tmp[j]+tmp[j+1]*2+tmp[j+2]*4+tmp[j+3]*8; // 满八减三
if(p>=8){
p-=3;
tmp[j+0]=bool(p&1);
tmp[j+1]=bool(p&2);
tmp[j+2]=bool(p&4);
tmp[j+3]=bool(p&8);
}
}
}
for(int i=0;i<512;i++){
bcd[i]=tmp[i];
}
return bcd;
}
void BCDToStr(int512 bcd,char* buf){ // bcd code to string
memset(buf,0,sizeof(buf));
for(int i=0;i<512;i+=4){
buf[i/4]='0'+bcd[i]+bcd[i+1]*2+bcd[i+2]*4+bcd[i+3]*8;
}
for(int i=127;i>=0;i--){
if(buf[i]!='0')break;
else buf[i]=0;
}
int len=strlen(buf);
std::reverse(buf,buf+len);
}
int512 BINToBCD(int512 bin){ // binary to bcd code
std::bitset<1024> tmp; // 由于数据范围,这里假设 bcd 码不超过 512 位。实际上是有可能超过 512 位的
tmp.reset();
for(int i=0;i<512;i++){
tmp[i]=bin[i];
}
for(int i=0;i<512;i++){
for(int j=512;j<1024;j+=4){
if(tmp[j+3]||tmp[j+2]&&(tmp[j+1]||tmp[j])){ // 满五加三,写法与上面不同
std::bitset<4>res; // 3 -> 0011
res[0]=tmp[j]^1;
res[1]=tmp[j]&1;
res[2]=(res[1]&tmp[j+1])||(tmp[j+1]&1)||(1&res[1]);
res[1]=tmp[j+1]^1^res[1];
res[3]=(res[2]&tmp[j+2])||(tmp[j+2]&0)||(0&res[2]);
res[2]=tmp[j+2]^0^res[2];
res[3]=tmp[j+3]^0^res[3];
tmp[j]=res[0],tmp[j+1]=res[1],tmp[j+2]=res[2],tmp[j+3]=res[3];
}
}
tmp<<=1;
}
for(int i=512;i<1024;i++){
bin[i-512]=tmp[i];
}
return bin;
}
int512 operator+(int512 a,int512 b){ // 加法,很简短 AwA
while(b.any()){
int512 t1=a^b,t2=a&b;
a=t1,b=t2<<1;
}
return a;
}
std::istream& operator>>(std::istream& in,int512 &a){ // 封装输入
in>>buf;
a=BCDToBIN(StrToBCD(buf[0]=='-'?buf+1:buf));
if(buf[0]=='-'){
int i=0;
while(a[i]==0){
i++;
}
i++;
while(i<512){
a[i]=!a[i];
i++;
}
}
return in;
}
std::ostream& operator<<(std::ostream& out,int512 a){ //·封装输出
if(a[511]==1){
out<<'-';
int i=0;
while(a[i]==0){
i++;
}
i++;
while(i<512){
a[i]=!a[i];
i++;
}
}
BCDToStr(BINToBCD(a),buf);
if(strlen(buf)==0){
buf[0]='0';
}
out<<buf;
return out;
}
int main(){ // 主函数
int512 a,b;
std::cin>>a>>b;
std::cout<<a+b;
}
这次代码可比上次长多了……真的是小题大做吧 [aru_39]
PS:站长已修改此博文
本文作者为vgakbzc,转载请注明。
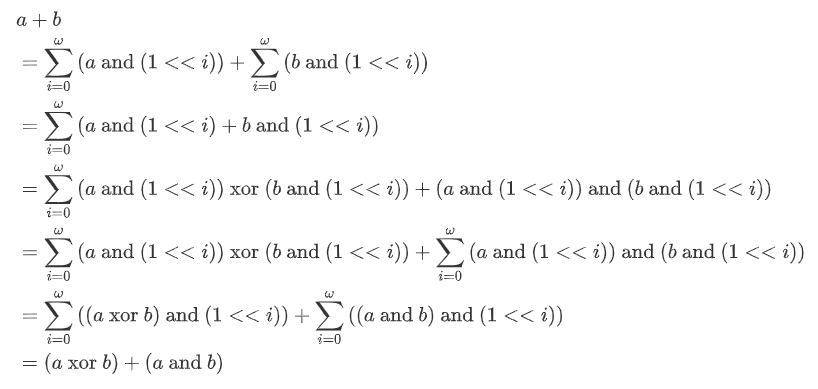

博主厉害,我都不会[emoji_38]
@光阴似箭我也没看懂呢 [aru_19]